Phase Encoding Steps

If each pixel is assigned a unique phase and frequency, why can't you use just a single phase-encoding step to decode spatial information?  
Although frequency components can be uniquely decoded by Fourier transformation from a single echo, the individual phase shifts contributed by each pixel cannot.  This non-uniqueness of phase information can be easily illustrated by the following example.
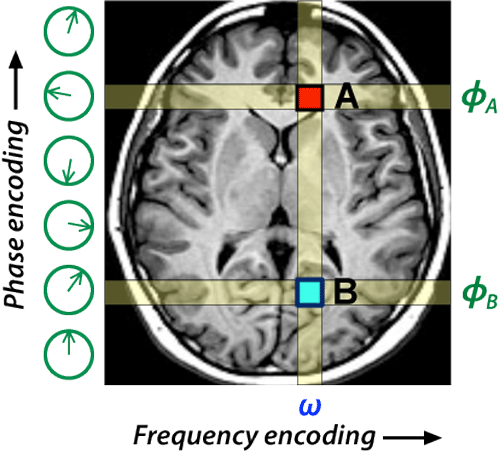
Consider two pixels, A and B, lying along the same frequency encoding column in an image, but with different gradient-induced phase shifts. Let pixel A generate an MR signal of the form A(t) =  sin(ωt + ϕA), and let pixel B generate a signal B(t) =  sin(ωt + ϕB).  

In an imaging experiment we measure an echo that contains the sum A(t) + B(t).  We now use a fundamental trigonometric identity about the sum of two sine waves (often learned in high school math, but forgotten): 
sin X + sin Y = 2 sin [½(X+Y)] cos [½(X−Y)]
Replacing X with (ωt + ϕA) and Y with (ωt + ϕB) and simplifying, we obtain:  
A(t) + B(t) = 2 sin [ωt + ½(ϕA+ϕB)] cos [½(ϕA−ϕB)] 
This equation shows that the combination of the signals (A + B) results in a sine wave of the same base frequency (ω), but with an averaged phase shift of ½(ϕA+ϕB).  From a single measurement we cannot determine the phase contributions from A or B individually.  For clinical MR imaging, therefore, multiple phase-encoding steps must be used to sort out spatial information in the phase-encoding direction.

Advanced Discussion (show/hide)»

References
     Lyons R. Sum of two sinusoids (pdf). (A nice little paper from dspguru.com that tabulates a variety of trigonometric identities for the sum of various combinations of sine and cosine waves).     
Related Questions
     I understand the 2-pixel example, but I still can't put it all together with the whole image and frequency encoding. Can you help?